Scala algorithm: Single-elimination tournament tree

Published

Algorithm goal

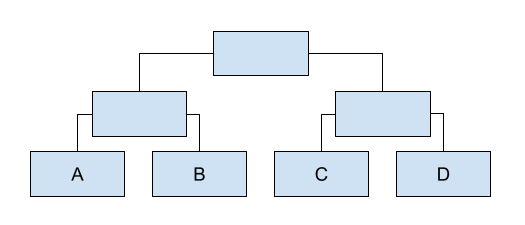
The single-elimination tournament is popular in team games. Represent a tournament tree which enables us to know what games to expect next, and who the overall winner of the tournament is, once the wins have been submitted. Here is a visual representation:

Test cases in Scala

assert(
  tourney.nextGames == Set(Drakas -> Lucas),
  "The first iteration has a specific next game"
)
assert(tourney.winner.isEmpty, "The first iteration does not have a winner")
assert(
  tourney.win(Sanzo).nextGames == tourney.nextGames,
  "A win by an unscheduled player does nothing to affect next games"
)
assert(
  tourney.win(Sanzo).winner.isEmpty,
  "A win by an unscheduled player does not give a new winner"
)
assert(
  tourney.win(Drakas).nextGames == Set(Drakas -> Sanzo),
  "A Drakas win pushes the next game to be Drakas v Sanzo"
)
assert(
  tourney.win(Drakas).winner.isEmpty,
  "A Drakas win still does not yield an overall winner"
)
assert(
  tourney.win(Drakas).win(Drakas).nextGames.isEmpty,
  "Drakas win 2x means final stage has no more expected games"
)
assert(
  tourney.win(Drakas).win(Drakas).winner.contains(Drakas),
  "Drakas win 2x means he is now set a winner of the tournament"
)

Algorithm in Scala

65 lines of Scala (compatible versions 2.13 & 3.0).

Get the full algorithm Scala algorithms logo, maze part, which looks quirky!

or

'Unlimited Scala Algorithms' gives you access to all the 100 published Scala Algorithms!

Upon purchase, you will be able to Register an account to access all the algorithms on multiple devices.

Stripe logo

Explanation

There are two aspects of this algorithm: first is to build the tree in-memory, the second is to process inputs in each iteration.

In building the tree, we take every 2 sibling players, and create a sub-tournament. Then each sibling sub-tournament gets combined with the next; we repeat until we are left with no siblings, and that becomes the root of our tournament tree. (this is © from www.scala-algorithms.com)

The leaf nodes are filled in, so they are 'DefinedPlayer', and those games that were not played yet are 'UndefinedPlayer'. Each 'UndefinedPlayer' has a left and a right, which represent the sub-trees that are either defined or not defined by themselves. When both children of an Undefined are defined, it means we now expect a face-off.

Full explanation is available to subscribers Scala algorithms logo, maze part, which looks quirky

Scala concepts & Hints

  1. Collect

    'collect' allows you to use Pattern Matching, to filter and map items.

    assert("Hello World".collect {
  case character if Character.isUpperCase(character) => character.toLower
} == "hw")

  2. Option Type

    The 'Option' type is used to describe a computation that either has a result or does not. In Scala, you can 'chain' Option processing, combine with lists and other data structures. For example, you can also turn a pattern-match into a function that return an Option, and vice-versa!

    assert(Option(1).flatMap(x => Option(x + 2)) == Option(3))

assert(Option(1).flatMap(x => None) == None)

  3. Pattern Matching

    Pattern matching in Scala lets you quickly identify what you are looking for in a data, and also extract it.

    assert("Hello World".collect {
  case character if Character.isUpperCase(character) => character.toLower
} == "hw")

  4. Stack Safety

    Stack safety is present where a function cannot crash due to overflowing the limit of number of recursive calls.

    This function will work for n = 5, but will not work for n = 2000 (crash with java.lang.StackOverflowError) - however there is a way to fix it :-)

    In Scala Algorithms, we try to write the algorithms in a stack-safe way, where possible, so that when you use the algorithms, they will not crash on large inputs. However, stack-safe implementations are often more complex, and in some cases, overly complex, for the task at hand.

    def sum(from: Int, until: Int): Int =
  if (from == until) until else from + sum(from + 1, until)

def thisWillSucceed: Int = sum(1, 5)

def thisWillFail: Int = sum(1, 300)

  5. State machine

    A state machine is the use of `sealed trait` to represent all the possible states (and transitions) of a 'machine' in a hierarchical form.

  6. Tail Recursion

    In Scala, tail recursion enables you to rewrite a mutable structure such as a while-loop, into an immutable algorithm.

    def fibonacci(n: Int): Int = {
  @scala.annotation.tailrec
  def go(i: Int, previous: Int, beforePrevious: Int): Int =
    if (i >= n) previous else go(i + 1, previous + beforePrevious, previous)

  go(i = 1, previous = 1, beforePrevious = 0)
}

assert(fibonacci(8) == 21)

Scala Algorithms: The most comprehensive library of algorithms in standard pure-functional Scala

How our 100 algorithms look

  1. A description/goal of the algorithm.
  2. An explanation with both Scala and logical parts.
  3. A proof or a derivation, where appropriate.
  4. Links to Scala concepts used in this specific algorithm, also unit-tested.
  5. An implementation in pure-functional immutable Scala, with efficiency in mind (for most algorithms, this is for paid subscribers only).
  6. Unit tests, with a button to run them immediately in our in-browser IDE.
Screenshot of an example algorithm demonstrating the listed features

Study our 100 Scala Algorithms: 6 fully free, 100 published & 0 upcoming

Fully unit-tested, with explanations and relevant concepts; new algorithms published about once a week.

  1. Compute the length of longest valid parentheses
  2. Check a binary tree is balanced
  3. Print a binary tree
  4. Remove duplicates from an unsorted List
  5. Make a queue using stacks (Lists in Scala)
  6. Find height of binary tree
  7. Single-elimination tournament tree
  8. Reverse Polish Notation calculator
  9. Quick Sort sorting algorithm in pure immutable Scala
  10. Check word in grid (depth-first search)
  11. Maximum wait at a fuel station
  12. Find minimum missing positive number in a sequence
  13. Least-recently used cache (LRU)
  14. Count pairs of a given expected sum
  15. Binary heap (min-heap)
  16. Compute a Roman numeral for an Integer, and vice-versa
  17. Compute keypad possibilities
  18. Matching parentheses algorithm with foldLeft and a state machine
  19. Traverse a tree Breadth-First, immutably
  20. Read a matrix as a spiral
  21. Remove duplicates from a sorted list (state machine)
  22. Token Bucket Rate Limiter
  23. Check word in grid (stack-safe)
  24. Leaky Bucket Rate Limiter
  25. Merge Sort: stack-safe, tail-recursive, in pure immutable Scala, N-way
  26. Median of two sorted arrays
  27. Longest increasing sub-sequence length
  28. Reverse first n elements of a queue
  29. Binary search a generic Array
  30. Game of Life
  31. Merge Sort: in pure immutable Scala
  32. Make a queue using Maps
  33. Is an Array a permutation?
  34. Count number of contiguous countries by colors
  35. Add numbers without using addition (plus sign)
  36. Tic Tac Toe MinMax solve
  37. Run-length encoding (RLE) Encoder
  38. Print Alphabet Diamond
  39. Find kth largest element in a List
  40. Balanced parentheses algorithm with tail-call recursion optimisation
  41. Reverse a String's words efficiently
  42. Count number of changes (manipulations) needed to make an anagram with an efficient foldLeft
  43. Count passing cars
  44. Count dist intersections
  45. Establish execution order from dependencies
  46. Counting inversions of a sequence (array) using a Merge Sort
  47. Longest common prefix of strings
  48. Check if an array is a palindrome
  49. Compute missing ranges
  50. Check a directed graph has a routing between two nodes (depth-first search)
  51. Compute nth row of Pascal's triangle
  52. Run-length encoding (RLE) Decoder
  53. Check if a number is a palindrome
  54. In a range of numbers, count the numbers divisible by a specific integer
  55. Merge intervals
  56. Compute minimum number of Fibonacci numbers to reach sum
  57. Find the longest palindrome within a string
  58. Find the index of a substring ('indexOf')
  59. Reshape a matrix
  60. Compute the steps to transform an anagram only using swaps
  61. Compute modulo of an exponent without exponentiation
  62. Closest pair of coordinates in a 2D plane
  63. Find the contiguous slice with the minimum average
  64. Compute maximum sum of subarray (Kadane's algorithm)
  65. Pure-functional double linked list
  66. Binary search in a rotated sorted array
  67. Check if a directed graph has cycles
  68. Rotate Array right in pure-functional Scala - using an unusual immutable efficient approach
  69. Check a binary tree is a search tree
  70. Length of the longest common substring
  71. Sliding Window Rate Limiter
  72. Tic Tac Toe board check
  73. Find an unpaired number in an array
  74. Check if a String is a palindrome
  75. Count binary gap size of a number using tail recursion
  76. Remove duplicates from a sorted list (Sliding)
  77. Monitor success rate of a process that may fail
  78. Least-recently used cache (MRU)
  79. Find sub-array with the maximum sum
  80. Find the minimum absolute difference of two partitions
  81. Find maximum potential profit from an array of stock price
  82. Fibonacci in purely functional immutable Scala
  83. Fizz Buzz in purely functional immutable Scala
  84. Find triplets that sum to a target ('3Sum')
  85. Find combinations adding up to N (non-unique)
  86. Find the minimum item in a rotated sorted array
  87. Make a binary search tree (Red-Black tree)
  88. Mars Rover
  89. Find combinations adding up to N (unique)
  90. Find indices of tuples that sum to a target (Two Sum)
  91. Count factors/divisors of an integer
  92. Compute single-digit sum of digits
  93. Fixed Window Rate Limiter
  94. Traverse a tree Depth-First
  95. Reverse bits of an integer
  96. Check Sudoku board
  97. Find k closest elements to a value in a sorted Array
  98. Print a binary tree vertically
  99. QuickSelect Selection Algorithm (kth smallest item/order statistic)
  100. Rotate a matrix by 90 degrees clockwise

Explore the 22 most useful Scala concepts

To save you going through various tutorials, we cherry-picked the most useful Scala concepts in a consistent form.

  1. Class Inside Class
  2. Class Inside Def
  3. Collect
  4. Def Inside Def
  5. Drop, Take, dropRight, takeRight
  6. foldLeft and foldRight
  7. For-comprehension
  8. Lazy List
  9. Option Type
  10. Ordering
  11. Partial Function
  12. Pattern Matching
  13. Range
  14. scanLeft and scanRight
  15. Sliding / Sliding Window
  16. Stack Safety
  17. State machine
  18. Tail Recursion
  19. Type Class
  20. Variance
  21. View
  22. Zip

Subscribe to Scala Algorithms

Maximize your Scala with disciplined and consistently unit-tested solutions to 100+ algorithms.

Use it from improving your day-to-day data structures and Scala; all the way to interviewing.

'Unlimited Scala Algorithms' gives you access to all the 100 published Scala Algorithms!

Upon purchase, you will be able to Register an account to access all the algorithms on multiple devices.

Stripe logo